Question

Part B: In complete sentences, explain how a circle can be used to find the circumcenter of the triangle graphed below.

Part C: Use a circle to locate the circumcenter of the triangle. Provide the location of the circumcenter.

Answer 1

Explanation:

Part B:

The center of the circumscribed circle around a triangle is equidistant from vertices of that triangle. To find the circumcenter need to draw at least two perpendicular bisectors to the sides of the given triangle. Point of intersect of them is center of the circumscribed circle.

Part C:

Coordinates of the midpoint of line BC ( y = - 1 ) are

(
`(-6+2)/(2)` ,
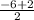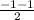`(-1-1)/(2)` ) = ( - 2 , - 1 ) and the equation of the line ⊥ to BC is x = - 2

Because BC is ║ to x-axis and m∠A is 90° , the center of the circle is midpoint of BC and r =
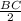`(BC)/(2)` = 4