Question

Evaluate, and round your answer to the nearest hundredth.

Answer 1

(d) -1.83

Explanation:

The explicit expression for the sum is ...

S = (-11/5)×(1 -(-1/5)^10)/(1 -(-1/5)) = -2.2(1 -1.024×10^-7)/1.2

S = -1.8333331456

The sum is approximately -1.83.

_____

Additional comment

For a sum of a sequence with multiplier 'a' and common ratio r, we find ...

`\displaystyle S=\sum_(n=1)^(10)ar^n=ar+ar^2+ar^3+\dots+ar^(10)\\\\rS=ar^2+ar^3+\dots+ar^(10)+ar^(11)\\\\S-rS=ar+(ar^2-ar^2)+(ar^3-ar^3)+\dots+(ar^(10)-ar^(10))-ar^(11)\\\\S=(ar-ar^(11))/(1-r)=ar(1-r^(10))/(1-r)`

__

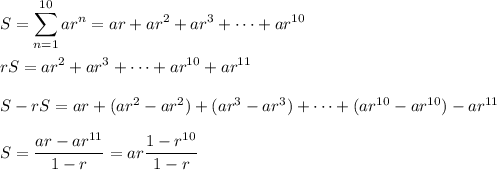
A calculator or spreadsheet can also find the sum for you.