Question

Suppose the path of a baseball follows the path graphed by the quadratic function ƒ(d) = –0.6d2 + 5.4d + 0.8 where d is the horizontal distance the ball traveled in yards, and ƒ(d) is the height, in yards, of the ball at d horizontal yards. Find the total horizontal distance the ball traveled while in the air.

A. 8.22 yards
B. 8.46 yards
C. 9.51 yards
D. 9.15 yards

Answer 1

The correct option D.

Explanation:

The given function is

`f(d)=-0.6d^2+5.4d+0.8`

Where f(d) is the height of the ball at horizontal distance d.

Put f(d)=0, to find the distance where the ball touch the ground.

`0=-0.6d^2+5.4d+0.8`

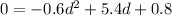
Quadratic formula:

`d=(-b\pm √(b^2-4ac))/(2a)`

Using the quadratic formula we get

`d=(-5.4\pm √((5.4)^2-4(-0.6)(0.8)))/(2(-0.6))`

`d=-0.146,9.146`

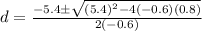
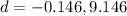
Therefore the ball is in air between d=-0.146 to d=9.146.

The distance can not be negative, therefore the ball remains in the air between d=0 to d=9.146.

`9.146\approx 9.15`

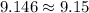
Therefore the correct option is D.