Question

Prove by mathematical induction that


`cos\theta+cos3\theta+cos5\theta+...+cos(2n-1)\theta=(sin2n\theta)/(2sin\theta)`
where sinθ≠0 for all positive integers n.

Answer 1

For
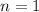`n=1`, on the left we have
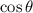`\cos\theta`, and on the right,

`(\sin2\theta)/(2\sin\theta)=(2\sin\theta\cos\theta)/(2\sin\theta)=\cos\theta`

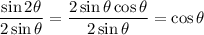
(where we use the double angle identity:
`\sin2\theta=2\sin\theta\cos\theta`)

Suppose the relation holds for
`n=k`:

`\displaystyle\sum_(n=1)^k\cos(2n-1)\theta=(\sin2k\theta)/(2\sin\theta)`

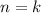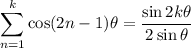
Then for
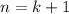`n=k+1`, the left side is

`\displaystyle\sum_(n=1)^(k+1)\cos(2n-1)\theta=\sum_(n=1)^k\cos(2n-1)\theta+\cos(2k+1)\theta=(\sin2k\theta)/(2\sin\theta)+\cos(2k+1)\theta`

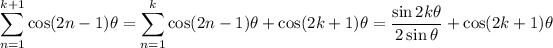
So we want to show that

`(\sin2k\theta)/(2\sin\theta)+\cos(2k+1)\theta=(\sin(2k+2)\theta)/(2\sin\theta)`

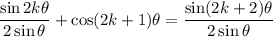
On the left side, we can combine the fractions:

`(\sin2k\theta+2\sin\theta\cos(2k+1)\theta)/(2\sin\theta)`

Recall that

`\cos(x+y)=\cos x\cos y-\sin x\sin y`

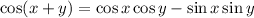
so that we can write

`(\sin2k\theta+2\sin\theta(\cos2k\theta\cos\theta-\sin2k\theta\sin\theta))/(2\sin\theta)`

`=(\sin2k\theta+\sin2\theta\cos2k\theta-2\sin2k\theta\sin^2\theta)/(2\sin\theta)`

`=(\sin2k\theta(1-2\sin^2\theta)+\sin2\theta\cos2k\theta)/(2\sin\theta)`

`=(\sin2k\theta\cos2\theta+\sin2\theta\cos2k\theta)/(2\sin\theta)`

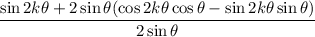
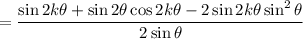
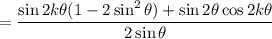
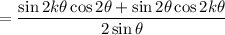
(another double angle identity:
`\cos2\theta=\cos^2\theta-\sin^2\theta=1-2\sin^2\theta`)

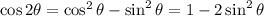Then recall that

`\sin(x+y)=\sin x\cos y+\sin y\cos x`

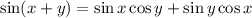
which lets us consolidate the numerator to get what we wanted:

`=(\sin(2k+2)\theta)/(2\sin\theta)`

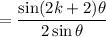
and the identity is established.