We first partition the interval [0, 2] into
 sub-intervals:
sub-intervals:
![\left[0,\frac2n\right],\left[\frac2n,\frac4n\right],\left[\frac4n,\frac6n\right],\ldots,\left[\frac{2(n-1)}n,2\right]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/kk1vxchbiqh1tbhqq9so98ckxyu6vmytji.png)
Notice how each sub-interval has length
 .
.
Since
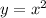 is an increasing function on the interval [0, 2] (which is evident from the fact that
is an increasing function on the interval [0, 2] (which is evident from the fact that
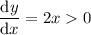 for
for
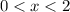 ), the circumscribed rectangles will have heights determined by the right endpoints of each sub-interval. This is to say, for the
), the circumscribed rectangles will have heights determined by the right endpoints of each sub-interval. This is to say, for the
 -th sub-interval, the area of the rectangle is
-th sub-interval, the area of the rectangle is
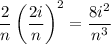
where
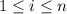 . So the area is approximated by the Riemann sum
. So the area is approximated by the Riemann sum
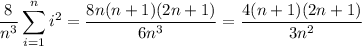
where the second equality makes use of the given hint, and we simplify from there.
The exact area is obtained by taking the limit as
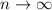 (and by definition is equivalent to the definite integral over [0, 2]):
(and by definition is equivalent to the definite integral over [0, 2]):
