Question

Suppose you want to transform the graph of the function into the graph of the function . Which transformations should you perform?

Answer 1

A) Reflect the graph of the first function across x-axis, translate it to the left, and translate it 2 units up.

Step-by-step explanation:

Hope you have a great day!

Answer 2

A. Reflect the graph of the first function across x-axis, translate it
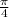`(\pi)/(4)` to the left, and translate it 2 units up.

Step-by-step explanation:

We have the original function is
`y=\tan (x+(\pi)/(4))-1`.

The new transformed function is given by
`y=-\tan (x+(\pi)/(2))+1`.

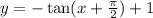So, we can see that the following sequence of transformations have been applied to the original function:

1. The function f(x) is reflected about x-axis i.e. f(x) becomes -f(x), which gives
`y=-\tan (x+(\pi)/(4))-1`

2. This function obtained is translated
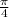`(\pi)/(4)` units to the left i.e.
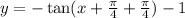`y=-\tan (x+(\pi)/(4)+(\pi)/(4))-1` i.e.
`y=-\tan (x+(\pi)/(2))-1`

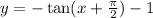
3. Finally, this new function is translated 2 units upwards i.e.
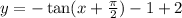`y=-\tan (x+(\pi)/(2))-1+2` i.e.
`y=-\tan (x+(\pi)/(2))+1`

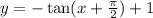
Hence, after applying, 'reflection across x-axis, translation of
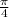`(\pi)/(4)` to the left, and translation of 2 units up', we get the required function.