Question

Two number cubes are rolled for two separate events:

Event A is the event that the sum of numbers on both cubes is less than 10.
Event B is the event that the sum of numbers on both cubes is a multiple of 3.
Complete the conditional-probability formula for event B given that event A occurs first by writing A and B in the blanks:


P( a0 |
a1) =
P( a2 ∩
a3)
P( a4)

Answer 1

Answer: The answer is
`(11)/(28).`

Step-by-step explanation: Given that two number cubes are rolled for two separate events A and B, where

A = the event that the sum of numbers on both cubes is less than 10

= {(1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2,1), (2,2), (2,3), (2,4), (2,5), (2,6), (3,1), (3,2), (3,3), (3,4), (3,5), (3,6), (4,1), (4,2), (4,3), (4,4), (4,5) ,(5,1), (5,2), (5,3), (5,4), (6,1), (6,2), (6,3)}

and

B =the event that the sum of numbers on both cubes is a multiple of 3

= {(1,2), (1,5), (2,1), (2,4), (3,3), (3,6), (4,2), (4,5), (5,1), (5,4), (6,3), (6,6) }

Let 'S' be the sample space for the experiment so that n(S) = 36.

Therefore, A and B = The event that the sum of numbers on both the cubes is less than 10 and multiple of 3

= {(1,2), (1,5), (2,1), (2,4), (3,3), (3,6), (4,2), (4,5) ,(5,1), (5,4), (6,3)}.

So, n(S) = 36, n(A) = 30, n(B) = 12 and n(A and B) = 11.

Hence, the conditional probability for the event B given that event A has already occured is given by

`P(B/A)=(P(B\cap A))/(P(A)),`

where,

`P(B\cap A)=(n(B\cap A)/(n(S))=(11)/(36).`

`P(A)=(n(A))/(n(S)=(28)/(36).`

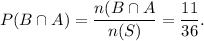
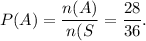
Therefore,

`P(B/A)=((11)/(36))/((28)/(36))=(11)/(28).`

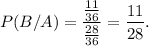
Thus, the required conditional probability is
`(11)/(28).`