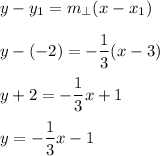Question

Write the equation of the line that is the perpendicular bisector of the segment with endpoints (4, 1) and (2, -5)

Answer 1

Answer:
`\bold{y=-(1)/(3)x-1}`

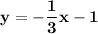
Explanation:

(4, 1) & (2, -5)

First, find the slope (m) and then the perpendicular (opposite reciprocal) slope:

`m=(y_2-y_1)/(x_2-x_1)\\\\\\m=(-5-1)/(2-4) = (-6)/(-2)=3\quad \rightarrow \quad m_(\perp)=-(1)/(3)\\`

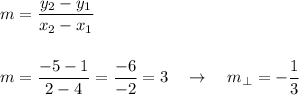
Next, find the midpoint of (4, 1) and (2, -5):

`Midpoint=\bigg((x_1+x_2)/(2),(y_1+y_2)/(2)\bigg)\\\\\\.\qquad \qquad=\bigg((4+2)/(2),(1-5)/(2)\bigg)\\\\\\.\qquad \qquad=\bigg((6)/(2),(-4)/(2)\bigg)\\\\\\.\qquad \qquad=(3, -2)`

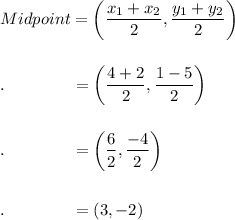
Lastly, input the perpendicular slope and the midpoint into the Point-Slope formula to find the equation of the line:

`y - y_1 = m_(\perp)(x - x_1)\\\\y - (-2) = -(1)/(3)(x - 3)\\\\y + 2=-(1)/(3)x +1\\\\y =-(1)/(3)x - 1\\`