Answer:
A.
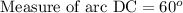
B.
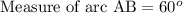
C.
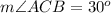
D.
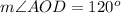
E.
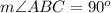
F.
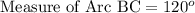
Explanation:
We have been given that the diameter AC of circle O is 24 cm. Arcs AB and CD are congruent. Angle DOC = 60° .
A. Since we know that the degree measure of an arc is equal to the measure of the central angle that intercepts the arc.
We can see that angle DOC is central angle and
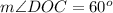 and arc DC subtends to central angle, therefore, the measure of arc DC will be 60 degrees.
and arc DC subtends to central angle, therefore, the measure of arc DC will be 60 degrees.
B. Since we are told that arcs AB and CD are congruent and measure of arc DC is 60 degrees, therefore, measure of arc AB will be 60 degrees as well.
C. The Inscribed Angle Theorem states that the measure of an inscribed angle is half the measure of its intercepted arc. Measure of Arc AB is 60 degrees, so by inscribed angle theorem the measure of angle ACB will be half the measure of AB.
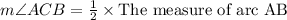
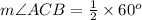
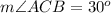
Therefore, measure of angle ACB will be 30 degrees.
D. We can see that angle DOC and AOD form a linear pair of angles, so they will add up-to 180 degrees.
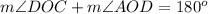
Upon substituting measure of angle DOC we will get,
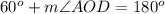
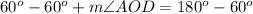
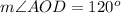
Therefore, measure of angle AOD will be 120 degrees.
E. Since we know that angle inscribed in a semicircle is always a right angle. We can see that angle ABC is angle inscribed in the semicircle as AC is the diameter of our given circle, therefore, measure of angle ABC will be 90 degrees.
F. Since we know that arc measure of a semicircle is 180 degrees. We can see that arc ABC is arc of the semicircle, so we can set an equation as:
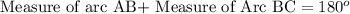
Upon substituting measure of arc AB we will get,
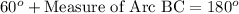
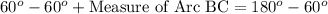
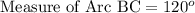
Therefore, measure of arc BC is 120 degrees.