Question

Omaha’s factory has yet another type of cost structure. Its cost function is provided graphically. Its maximum capacity is 38,000 units per day.

part a. At what rate is the cost per unit decreasing for production levels above 12,000?


part b. State the function for the domain over [12000, 38000].



part c. What is the cost per unit at the production level of 19,000?

Omaha’s city council approved a special growth incentive that decreases the company’s tax burden for production levels above last year’s average. Explain how this is reflected by the Cost Function for Omaha’s factory.

Answer 1

Part a. The cost per unit decreasing by 0.00001 for production levels above 12,000.

Part b. The function for the domain over [12000, 38000] is
`y=-0.00001x+0.97`.

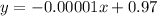Part c. The cost per unit at the production level of 19,000 is 0.78.

Step-by-step explanation:

Part a.

From the given graph it is clear that the graph passes through the points (12000,0.85) and (38000,0.59).

If a line passes through two points then the slope of the line is

`m=(y_2-y_1)/(x_2-x_1)`

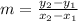
The rate of change in cost per unit for production levels above 12,000 is

`m=(0.59-0.85)/(38000-12000)=-0.00001`

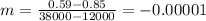
Here negative sign represents the decreasing rate. It means the cost per unit decreasing by 0.00001 for production levels above 12,000.

Part b.

The point slope form of a linear function is

`(y-y_1)=m(x-x_1)`

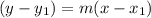
Where, m is slope.

The slope of the line over [12000, 38000] is -0.00001 and the point is (12000,0.85). So, the function for the domain over [12000, 38000] is

`(y-0.85)=-0.00001(x-12000)`

`(y-0.85)=-0.00001x+0.012`

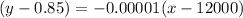
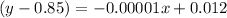
Add 0.85 on both the sides.

`y=-0.00001x+0.12+0.85`

`y=-0.00001x+0.97`

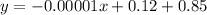
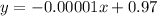
The function for the domain over [12000, 38000] is y=-0.00001x+0.97.

Part c.

Substitute x=19000 in the above equation, to find the cost per unit at the production level of 19,000.

`y=-0.00001(19000)+0.97=0.78`

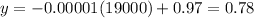
Therefore the cost per unit at the production level of 19,000 is 0.78.