Answer:
Part a. The cost per unit decreasing by 0.00001 for production levels above 12,000.
Part b. The function for the domain over [12000, 38000] is
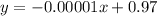 .
.
Part c. The cost per unit at the production level of 19,000 is 0.78.
Step-by-step explanation:
Part a.
From the given graph it is clear that the graph passes through the points (12000,0.85) and (38000,0.59).
If a line passes through two points then the slope of the line is

The rate of change in cost per unit for production levels above 12,000 is
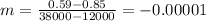
Here negative sign represents the decreasing rate. It means the cost per unit decreasing by 0.00001 for production levels above 12,000.
Part b.
The point slope form of a linear function is
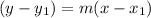
Where, m is slope.
The slope of the line over [12000, 38000] is -0.00001 and the point is (12000,0.85). So, the function for the domain over [12000, 38000] is
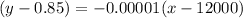
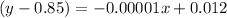
Add 0.85 on both the sides.

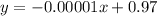
The function for the domain over [12000, 38000] is y=-0.00001x+0.97.
Part c.
Substitute x=19000 in the above equation, to find the cost per unit at the production level of 19,000.
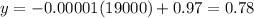
Therefore the cost per unit at the production level of 19,000 is 0.78.