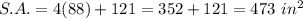Question

What is the surface area

Answer 1

473 in²

Explanation:

We have four congruent triangles and a square in the base.

The formula of an area of a triangle:

`A_\triangle=(1)/(2)bh`

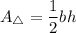
b - base

h - height

The formyla of an area of a square:

`A_{\boxed{}}=a^2`

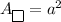
a - length of side

We have b = 11 in, h = 16 in and a = 11 in. Substitute:

`A_\triangle=(1)/(2)(11)(16)=(11)(8)=88\ in^2\\\\A_{\boxed{}}=11^2=121\ in^2`

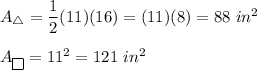
The Surface Area :

`S.A.=4A_\triangle+A_{\boxed{}}`

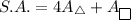
Substitute:

`S.A.=4(88)+121=352+121=473\ in^2`