Question

Graph this rational equation. Identify the points of discontinuity, holes, vertical asymptotes, x-intercepts, and horizontal asymptote.

f(x)=x-2/x-4

Explain how created your graph and describe the points of discontinuity, holes, vertical asymptotes, x-intercepts, and horizontal asymptote of each



Please explain how you got the answer. Thank you.

Answer 1

Explanation:

We have given,

A rational function : f(x) =
`(x-2)/(x-4)`

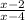
W need to find :

Point of discontinuity : - At x = 4, f(x) tends to reach infinity, So we get discontinuity point at x =4.

For no values of x, we get indetermined form (i.e
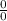`(0)/(0)`), Hence there is no holes

Vertical Asymptotes:

Plug y=f(x) = ∞ in f(x) to get vertical asymptote {We can us writing ∞ =
`(1)/(0)`}

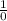i.e ∞ =
`(x-2)/(x-4)`

or
`(1)/(0)=(x-2)/(x-4)`

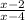
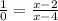
or x-4 =0

or x=4, Hence at x = 4, f(x) has a vertical asymptote

X -intercept :

Plug f(x)=0 , to get x intercept.

i.e 0 =
`(x-2)/(x-4)`

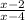
or x - 2 =0

or x = 2

Hence at x=2, f(x) has an x intercept

Horizontal asymptote:

Plug x = ∞ in f(x) to get horizontal asymptote.

i.e f(x) =
`(x-2)/(x-4)` =
`(x(1-(2)/(x) ))/(x(1-(4)/(x) ))`

or f(x) =
`((1-(2)/(∞) ))/((1-(4)/(∞) ))`

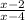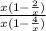
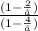
or f(x) = 1 = y

hence at y =f(x) = 1, we get horizontal asymptote