Answer:
(a)
S={m∈ real numbers|
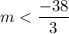 }
}
(b)
S=
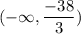
Explanation:
The inequality is given as:
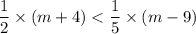
Now on solving this inequality we have:
firstly we multiply both side by 10 and then combine the like terms in order to obtain our inequality:
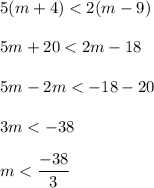
Hence, the solution set of the following inequality is the set of all those real numbers such that
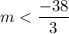
(a)
The solution set(S) in the set-builder notation could be represented as:
S={m∈ real numbers|
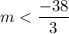 }
}
(b)
In interval notation we can write our solution set as:
S=
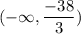
(c)
The graph of the solution set is attached to the answer.