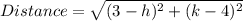Answer:
The correct answer is:
2)
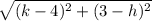
3)
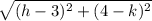
4)
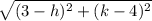
5)
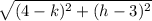
Explanation:
We can find the distance between two points with the help of the distance formula.
The distance between two points (a,b) and (c,d) is calculated by the formula:
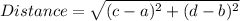
which is similar to the expression:
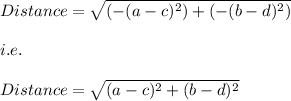
or

or
Distance=\sqrt{(c-a)^2+(b-d)^2}[/tex]
Here we are asked to find the distance between the point A(3,k) and B(h,4)
The distance is given by:
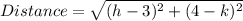
which is also written by:
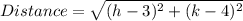
or
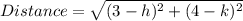
or