Answer:
D) Consistent and Independent
Explanation:
The system of equations,
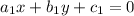 and
and
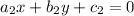
is consistent and independent if
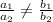
The system is consistent and dependent if
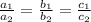
The system is inconsistent if
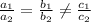
Now, in the given system
4x - y + 3 = 0 and
2x - y - 4 = 0
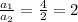
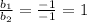
So,

Hence, the given system is consistent and independent.