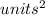Question

Can someone please help me with this. one this question i need help finding the area.

Answer 1

Area = 86.088
`units ^ 2`

Explanation:

The first thing you need to find the area of the rectangles is to find the length of two of its sides.

To do this, identify by means of the graph in which points are their vertices.

In the attached image these points are identified.

First we must find the distance AB.

For this we use the formula of the distance between two points:

`AB = √((3-(-7))^2 + (3 - 6)^2)`

`AB = 10.44`

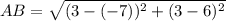
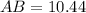
Now we find the distance AC

`AC = √((-9-(-7))^2 + (-2-6)^2)`

`AC = 8.246`

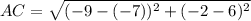
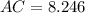
Finally the area of a rectangle is equal to the product of its base because of its height. So:

Area = AB(AC)

Area = 10.44(8,246)

Area = 86.088
`units ^ 2`