Question

A rectangular sandbox has a width that's 1⁄4 of its length. The total area of the sandbox is 36 square feet. Find the dimensions of the sandbox

Answer 1

Dimensions of box

Length is 12 feet

Width is 3 feet

Explanation:

Let's assume length of sandbox is L

width of box is W

we are given

A rectangular sandbox has a width that's 1⁄4 of its length

so, we can write as

`W=(1)/(4)L`

we know that

area = length*width

so, we get

`A=L* W`

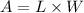
now, we can plug back W

`A=L* (1)/(4)L`

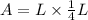
we can set Area=36

`36=L* (1)/(4)L`

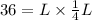
now, we can solve for L

`L^2=144`

`L=12`

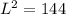
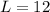
now, we can find W

`W=(1)/(4)* 12`

`W=3`

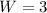
So, dimensions of box

Length is 12 feet

Width is 3 feet