Question

Two circles, each of radius 5 units, have centers at the origin and at (7, 7), respectively. what is the y-intercept of the line that contains their common chord?

Answer 1

Hence, the y-intercept of the line that contains their common chord is 7.

Explanation:

The equation of the first circle is:

`x^2+y^2=5^2`

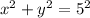
and the equation of the second circle is:

`(x-7)^2+(y-7)^2=5^2`

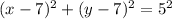
When we plot the two circle they intersect each other at two points and the point of intersection are (3,4) and (4,3).

Hence, the chord of the two circles will also pass through these two points and in order to get the y-intercept of the line or the chords of the two circles we need to find the equation of line that passes through these two points:

Hence the equation of line passing through (a,b) and (c,d) is given by:

`y-b=(d-b)/(c-a)* (x-a)`

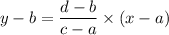
we have (a,b)=(3,4) and (c,d)=(4,3)

`y-4=(3-4)/(4-3)* (x-3)\\ \\y-4=-1(x-3)\\\\y-4=-x+3\\\\x+y=3+4\\\\x+y=7`

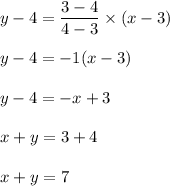
The y-intercept of a line is the point where x=0.

Hence when x=0,

y=7

Hence, the y-intercept of the line that contains their common chord is 7.