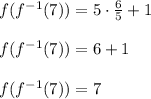Question

For f(x) = 5x + 1

A. Find f(7).
B. Find f^−1 (x).
C. Find f^−1 (7).
D. Find f( f^−1 (7)).
Show your work.

Answer 1

`A)\\f(x)=5x+1\\\\f(7):\ \text{Put x = 7 to the equation of the function:}\\\\f(7)=5(7)+1=35+1=36\\\\\boxed{f(7)=36}`

`B)\\f(x)=5x+1\to y=5x+1\\\\\text{exchange x to y}\\\\x=5y+1\\\\\text{solve for y}\\\\5y+1=x\qquad\text{subtract 1 from both sides}\\\\5y=x-1\qquad\text{divide both sides by 5}\\\\y=(1)/(5)x-(1)/(5)\\\\\boxed{f^(-1)(x)=(1)/(5)x-(1)/(5)}`

`C)\\f^(-1)(x)=(1)/(5)x-(1)/(5)\\\\f^(-1)(7):\ \text{Put x = 7 to the equation of the function}\ f^(-1)(x):\\\\f^(-1)(7)=(1)/(5)(7)-(1)/(5)=(7)/(5)-(1)/(5)=(7-1)/(5)=(6)/(5)=1(1)/(5)\\\\\boxed{f^(-1)(7)=1(1)/(5)}`

`D)\\f(f^(-1)(7))\\\\f^(-1)(7)=(6)/(5),\ \text{Therefore put}\ x=(6)/(5)\ \text{to the equation of the function}\ f(x):\\\\f\left((6)/(5)\right)=5\left((6)/(5)\right)+1=6+1=7\\\\\boxed{f(f^(-1)(7))=7}`

Answer 2

A . 36

B.
`f^(-1)(x)=(1)/(5)(x-1)`

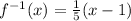
C. 6/5

D. 7

Explanation:

We have been given the function
`f(x)=5x+1`

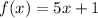
A. Substitute x = 7 in the given function

`f(7)=5(7)+1\\f(7)=36`

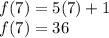
B. Let us find the inverse of the function

`f(x)=5x+1\\y=5x+1`

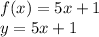
Interchange x and y, we get

`x=5y+1`

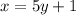
Solve for y

`x-1=5y\\\\y=f^(-1)(x)=(1)/(5)(x-1)`

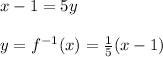
C. Substitute x= 7, in the inverse function

`f^(-1)(7)=(1)/(5)(7-1)\\\\f^(-1)(7)=(6)/(5)`

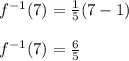
D. Substitute x = 6/5 in the given function, we get

`f(f^(-1)(7))=5\cdot (6)/(5) +1\\\\f(f^(-1)(7))=6+1\\\\f(f^(-1)(7))=7`