Answer:
Option D. AC= 10 cm and CE= 5 cm
Explanation:
From the given figure two triangles ΔABC and ΔADE are similar and two lines BC║DE.
From these similar triangles we know

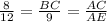
Therefore
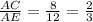
Or AC=
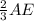
Now from pythagoras theorem
AE = √(AD²+ED²) = √(12²+9²) = √(144+81) =√225 = 15 cm
Since we know side AC =
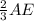
=
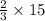
= 10 cm
Therefore AC = 10 cm and AE = 15cm and CE = (15-10) = 5 cm