Question

a 14 kg rock starting from rest free falls through a distance of 5.0 m with no air resistance. find the momentum change of the rock caused by its fall and the resulting change in the magnitude of earths velocity. earth mass is 6.0 * 10^24 kg. show your work assuming the rock earth system is closed.

Answer 1

To find the momentum change of a rock in free fall, calculate the final velocity using v = √(2gh) and multiply by the mass. The momentum change of the Earth is equal and opposite but negligibly small due to its large mass.

Step-by-step explanation:

To calculate the momentum change of a 14 kg rock that falls 5.0 m, we’ll use the laws of physics for free fall and conservation of momentum. Initially, as the rock is at rest, its momentum is 0. When it hits the ground, the velocity can be found using the formula for the final velocity of a falling object: v = √(2gh), where g is the acceleration due to gravity (9.8 m/s2) and h is the height (5.0 m). Calculating the velocity, we have v = √(2 * 9.8 m/s2 * 5.0 m) = √(98 m2/s2) = 9.9 m/s. The momentum just before impact, p, is mass (m) times velocity (v): p = m * v = 14 kg * 9.9 m/s = 138.6 kg·m/s.

Since momentum is conserved in a closed system, the Earth will experience an equal and opposite change in momentum. However, due to Earth’s massive size (6.0 * 1024 kg), the resulting change in its velocity is negligibly small but theoretically equal in magnitude to the momentum change of the rock.

Answer 2

`2.3*10^(-23) m/s`

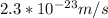
Step-by-step explanation:

Momentum (p) is defined as the product of the mass (m) and velocity (v) of an object:

`p=mv`

There are different types of momentum. Linear momentum (caused by the linear motion of te rock) and angular momentum (caused by the angular velocity of the earth).

Initial momentum of the falling rock equals zero, because its initial velocity is zero. To find the momentum change, we need its final value, for which we need its final velocity.

The kinematic formula, which relates final velocity (v), initial velocity (v0), acceleration (a) and falling distance (h) is:

`v^(2)=v_(0) +2ah`

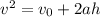
In this case:

`v^2=0+2(9.8m/s^2)(5.0m)=98m^2/s^2`

`v=√(98m^2/s^2)`

`v=9.9m/s`

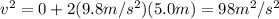
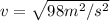
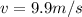
Now, the change in momentum (dp) of the rock is simply is simply:

`dp=m*v-m*v_(0)=m(v-v_(0))`

`dp=14kg(9.9m/s-0m/s)=139kg*m/s`

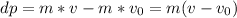
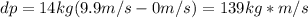
For closed systems (like this earth-rock system), momentum is conserved. It means that a change in rock's momentum equals to an opposite but in the same magnitude momentum change of the earth. The initial momentum of the earth is also equal to zero. Matching changes in momentum:

`dP_(rock)=dP_(earth)\\14kg*9.9m/s=6.0*10^(24) kg*v`

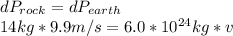
Solving for v:

`v=2.3*10^(-23) m/s`

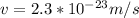
The, the change in earth's speed magnitude is 2.3*10^-23m/s