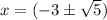Answer:
Option b)
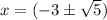 .
.
Explanation:
We have to solve the equation x²+6x+4 =0 for the value of x.
As we know from any quadratic equation ax²+bx+c=0
the value of
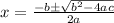
Now with the help of this formula we will solve the equation
x²+6x+4 = 0
By putting the values of a= 1, b=6, c=4 in the formula
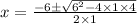
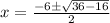
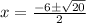
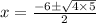
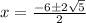
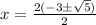
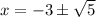
so the final answer is