Question

The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary Prove that the height of the tower is 6 m.

Kindly help!​

Answer 1

Proof explained below

Explanation:

Tan trigonometric ratio

`\sf \tan(\theta)=(O)/(A)`

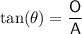
where:

• 
  `\theta` is the angle
• O is the side opposite the angle
• A is the side adjacent the angle

Draw a diagram to help visualize the scenario (see attached).

If the angles are complementary, their sum is 90°.

Therefore, let one of the angles be
`x` and the other angle be
`90^(\circ)-x`.

Use the tan trig ratio to create two equations with the missing side length.

Right triangle ACD

Given:

• 
  `\theta = x`
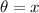
• O = CD (tower)
• A = 9 m

Substituting the given values into the tan trig ratio:

`\implies \tan (x)= \frac{\textsf{CD}}{9}`

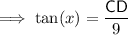
Right triangle BCD

Given:

• 
  `\theta = 90^(\circ) - x`
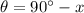
• O = CD (tower)
• A = 4 m

Substituting the given values into the tan trig ratio:

`\implies \tan (90^(\circ) - x)= \frac{\textsf{CD}}{4}`

`\textsf{As }\:\tan(90^(\circ) - x)= \cot (x):`

`\implies \cot(x)= \frac{\textsf{CD}}{4}`

`\implies (1)/(\tan(x))= \frac{\textsf{CD}}{4}`

`\implies \tan(x)= \frac{4}{\textsf{CD}}`

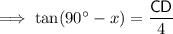
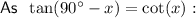
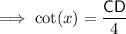
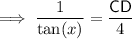
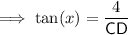
Therefore, the two equations are:

`\textsf{Equation 1}: \quad \tan (x)= \frac{\textsf{CD}}{9}`

`\textsf{Equation 2}: \quad \tan(x)= \frac{4}{\textsf{CD}}`

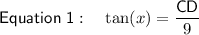
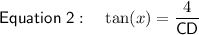
Substitute one equation into the other and solve for CD:

`\implies \sf (CD)/(9)=(4)/(CD)`

`\implies \sf CD \cdot CD= 4 \cdot 9`

`\implies \sf CD^2=36`

`\implies \sf CD=√(36)`

`\implies \sf CD= \pm 6`

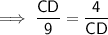
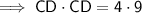
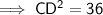
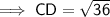
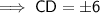
As distance cannot be negative, CD = 6 m only, thus proving that the height of the tower is 6 m.