Answer: The correct answers are

Step-by-step explanation:
To find the polynomials which could represent the are of a square having side x greater than 2, we need to find the value of 'x' for all the given polynomials.
From the given options:
- 1.

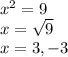
x = -3 is ignored.
- 2.
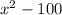
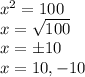
x = -10 is ignored
- 3.
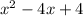
To solve this we use the quadratic formula:
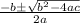
Putting values of a, b and c, we get:

As, x comes out to be 2 and is not greater than 2. Hence, this is not considered.
- 4.
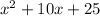
Solving for 'x' by splitting the middle term:
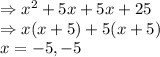
Hence, this is ignored.
- 5.
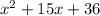
Solving for 'x' by splitting the middle term:

Hence, this is ignored.
So, the correct polynomials are
