
has characteristic equation
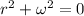
with roots at
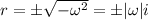 , hence the characteristic solution is
, hence the characteristic solution is
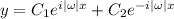
or equivalently,
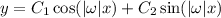
With the given boundary conditions, we require
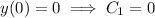
and
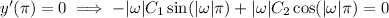
With
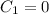 , the second condition reduces to
, the second condition reduces to
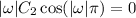
Assuming
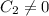 (because we don't want the trivial solution
(because we don't want the trivial solution
 ), it follows that
), it follows that
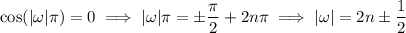
where
 is an integer. In order to ensure
is an integer. In order to ensure
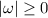 , we must have
, we must have
 if
if
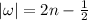 , or
, or
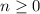 if
if
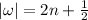 .
.