Question

The dollar value v(t) of a certain car model that is t years old is given by the following exponential function. v(t)=27500(0.88)^t Find the initial value of the car and the value after 13 years. Round your answers to the nearest dollar as necessary.

Answer 1

Current value is $27500 and the value after 13 years will be $20417.

Explanation:

The dollar value v(t) of a certain car model in t years is given by the exponential function
`v(t)=27500*(0.88)^(t)`

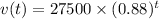
Now we have to find the initial value and the value after 13 years.

Therefore to calculate the initial value of the car v(0)=27500\times(.88)^{0}

= 27500×1 (since
`x^(0)=1`

So the current value of the car is $27500.

Now we will calculate the value of car after 13 years.

v(13) =
`27500(0.88)^(13)`

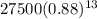
Now we take the log on both the sides of the equation

`logv(13)=log\left \{ 27500* (.88)^(13) \right \}`

`=log 27500+13log(.88)`

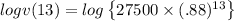
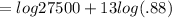
= 4.44 + 13log(88÷100)

= 4.44 + 13( log88 - log100)

= 4.44+ 13(1.94-2)

log v(13)= 4.44 - 13(.056)

= 4.44- 0.72

= 3.72

⇒ v(13) =
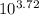`10^(3.72)` = 20417.38 ≈ $20417

Answer 2

Answer: Initial value of car = $ 27500

And, the value of car after 13 years is $5219.242

Explanation:

Here, the given function that models the price of car after t years,

`v(t) = 27500(0.88)^t`

Since, initially, t = 0

Thus, the initial value of the car,

`v(0) = 27500(0.88)^0=27500`

Now, after 13 years, t = 13

Thus, the value of car after 13 years,

`v(13)=27500(0.88)^(13)`

=
`27500* 0.189790617123`

=
`5219.24197088\approx 5219.242`