Answer: x = 28 unit
Explanation:
Here, In triangle APR,
CD ║ AP,
Such that, C ∈ AR and D ∈ PR,
Also, AC = 10 unit, CR = x unit, PD = 15 unit and DR = 42 unit,
Since, CD ║ AP,
Thus, by the alternative interior angle theorem,
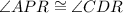
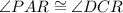
Thus, By AA similarity postulate,
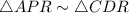
Since, the corresponding sides of the similar triangle are in same proportion,
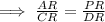
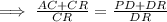
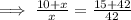
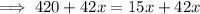
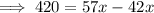
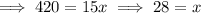
Hence, the value of x = 28.