Question

Choose the function that correctly identifies the transformation of f(x) = x2 shifted three units to the left and five units up. g(x) = (x - 3)2 - 5 g(x) = (x - 3)2 + 5 g(x) = (x + 3)2 + 5 g(x) = (x + 3)2 - 5

Answer 1

c

Explanation:

Answer 2

Answer:
`g(x) = (x+3)^2 + 5`

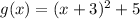
Explanation:

Here, the given function,

`f(x) = x^2`

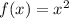
Which is the equation of parabola, having vertex (0,0)

When the function f(x) is transformed to a new function,

Then we can write the new equation of parabola,

`g(x) = a(x-h)^2+k^2`

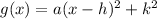
Where h shows the horizontal shifting and k shows the vertical shifting

While a shows the compression,

Here compression is not occur.

Therefore, a = 1

Now, f(x) is shifted three unit to the left

Therefore, h = - 3 ( In left side we take negative shifting)

Again, f(x) is shifted five unit up,

k = 5

(Note: In case of downward shifting the value of k will be negative)

By putting the values of a, h and k in the above transformed equation,

We get,
`g(x) = (x+3)^2 + 5`

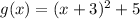
Which is the required transformed equation.

⇒ Third Option is correct.