Answer:
 by SAS.
by SAS.
Explanation:
From the graph, we see that
 by SAS, because
by SAS, because
 ,
,
 and
and
 , so by this given elements, we use Side-Angle-Side postulate.
, so by this given elements, we use Side-Angle-Side postulate.
To demonstrate the congruence between angles, we know by given
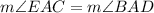
By sum of angles, we have
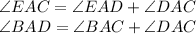
Replacing this sum of angles in the first expression, we have
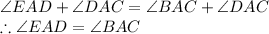
So, by SAS,
