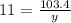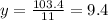Question

The values (9.4,11) and (11,y) are from an inverse variation. Find the missing value and round to the nearest hundredth.

Answer 1

0.94

Step-by-step explanation:

We know that the given values (9.4,11) and (11,y) are from an inverse variation.

So we can write the function of an inverse variation as:

`y` ∝
`\frac{1} {x}`

`y = \frac {k} {x}`

Finding the constant
`k`:

`11 = \frac {k}{9.4}`

`k = 9.4*11`

`k = 10.34`

Now finding the missing value
`y`:

`y = \frac {10.34}{11}`

`y = 0.94`

Therefore, the missing value is (11, 0.94).

Answer 2

Answer: 9.4

Step-by-step explanation:

Here the x-coordinates and y-coordinates have the inverse relation.

⇒
`x\propto(1)/(y)`

⇒
`x=(k)/(y)`

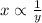
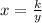
Where k is variation constant.

Since, point (9.4, 11) is from the inverse variation,

Therefore, this point must be satisfy the above condition,

That is,
`9.4=(k)/(11)`

`k=103.4`

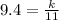
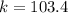
Thus, the relation between the coordinates is,

`x=(103.4)/(y)`

Put x = 11, in the above function,

`11=(103.4)/(y)`

`y=(103.4)/(11)=9.4`