Suppose that x and y vary inversely and that y=1/6 when x=3. Write a function that models the inverse variation and find y when x=10.

Question

asked Oct 11, 2020 37.5k views

2 Answers

Jonnow · Answer 1 · 2020-10-13T17:43:07+0000

Answer:

y = 1/20 when x = 10

Explanation:

We know that x and y vary inversely and
y=(1)/(6) when
x=3 .

So we can write the function of an inverse variation as:

∝
$\frac{1} {x}$

$y = \frac {k} {x}$

Finding the constant
:

(1)/(6) =(k)/(3)

k=(1)/(6)*3

k=(1)/(2)

Now finding the missing value
:

y=((1)/(2))/(10)

y = (1)/(2) * (1)/(10)

y = (1)/(20)

Therefore, the missing value is
(10, (1)/(20) ) .

Charnel · Answer 2 · 2020-10-15T17:30:27+0000

Answer:

The Inverse variation states a relationship between the two variable in which the product is constant.

i.e
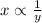
$x \propto (1)/(y)$

then the equation is of the form:
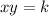xy = k where k is the constant of variation.

As per the given information: It is given that x and y vary inversely and that y = 1/6 when x = 3.

then, by definition of inverse variation;

xy = k ......[1]

Substitute the given values we have;

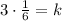
$3 \cdot (1)/(6) = k$

(1)/(2) = k

Now, find the value of y when x = 10.

Substitute the given values of x=10 and k = 1/2, in [1] we have;

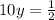
10y = (1)/(2)

Divide both sides by 10 we get;

y = (1)/(20)

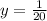
therefore, a function that models the inverse variation is;
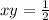and value of
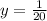when x = 10.