Answer: The correct option is (C)

Step-by-step explanation: We are given to find the equation of the line that is parallel to the given line in the graph and passes through the point (−4,−6 ).
We can see from the graph that
the line passes through the points (-8, 4) and (8, 4). So, the slope of the graphed line is
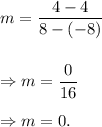
The line parallel to the graphed line will also have slope m = 0 because parallel lines have same slopes.
Since the new line passes through the point (-4, -6), so its equation will be

Thus, the required equation of the line is

Option (C) is CORRECT.