Mechanical energy of the ball will remain conserved
so here we have
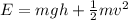
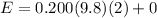
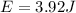
so mechanical energy will remain same at all positions
Now when ball comes to position of 1 m height then potential energy is given as
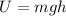

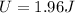
Now since total mechanical energy is conserved so we will say
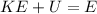
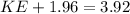
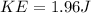
so we have
its mechanical energy = 3.92 J
its potential energy = 1.96 J
its kinetic energy = 1.96 J