Question

Find the angles of the rhombus if the ratio of the angles formed by diagonals and the sides of the rhombus is 6:5.

Answer 1

Answer:
`((1080)/(11))^(\circ)` and
`((900)/(11) )^(\circ)`

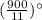
Explanation:

Here, the ratio of the angles formed by diagonals and the sides of the rhombus is 6:5.

Let the angles formed by diagonals and the sides of the rhombus are 6x and 5x.

Where x is any number.

Therefore, the angles of rhombus are = 12 x and 10x ( Because in rhombus opposite angles are equal and diagonals are the angle bisectors in case of rhombus)

Also, In rhombus diagonals bisect each other perpendicularly.

`6x + 5x + 90^(\circ) = 180^(\circ)`

`\implies 11 x + 90^(\circ) = 180^(\circ)`

`\implies 11x = 90^(\circ)`

`\implies x = (90)/(11)`

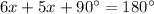
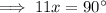
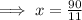
⇒ The one angle of rhombus =
`(6* (90)/(11))^(\circ)=((540)/(11))^(\circ)`

And another angle =
`(5* (90)/(11))^(\circ)=((450)/(11))^(\circ)`