Answer:
Option (b) is correct.
Using the Zero-Product Property, on the given equation
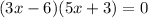 we get,
we get,
 and
and

Explanation:
Consider the given equation ,
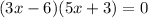
Zero- product property states that if the product of two term is zero then either first term is zero or second term is zero
That is
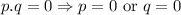
Consider the given equation ,
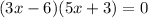
Applying zero-product property, we get,
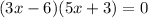
this implies that either
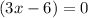 or
or
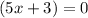
either
 or
or

Thus, using the Zero-Product Property, on the given equation
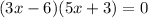 we get,
we get,
 and
and
 .
.