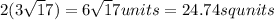Question

The coordinates of the vertices of a rectangle are (-8,2),(0,4),(1,0), and (-7,-2)

What is the perimeter of the rectangle? Round each step to the nearest tenth.
Enter your answer in the box.
___ units

Answer 1

Perimeter of rectangle =24.7 units

Explanation:

From the figure, Perimeter of the rectangle=
`2(length+breadth)`

=
`2(BC+CD)`

Now, BC=
`\sqrt{(0-1)^(2)+(4-0)^(2)}=√(1+16)=√(17)=4.1 units`

and CD=
`\sqrt{(1+7)^(2)+(0+2)^(2)}=√(64+4)=√(68)=8.2 units`

Therefore,perimeter of the rectangle=
`2(4.1+8.2)=2(12.3)=24.7 units`.

Answer 2

Perimeter of rectangle is 24.74 squnits.

Explanation:

Given The coordinates of the vertices of a rectangle are (-8,2),(0,4),(1,0), and (-7,-2). we have to find the perimeter of rectangle.

As we know,

Perimeter of rectangle=2(L+B)

Length of rectangle=
`√((0+8)^2+(4-2)^2)=\sqrt64+4=\sqrt68=2\sqrt17`

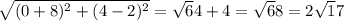
Breadth of rectangle=
`√((1-0)^2+(0-4)^2)=\sqrt1+16=\sqrt17`

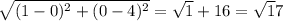
Now, Perimeter=
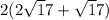
`2(2\sqrt17+\sqrt17)`

=
`2(3\sqrt17)=6\sqrt17units=24.74 squnits`