Answer:
The required solutions are a.
 , b.
, b.
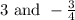 , c.
, c.
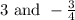 .
.
Explanation:
a.
The given quadratic equation is
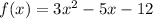
The middle term can be written as (-9x+4x)
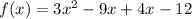
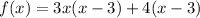

The intercept form of the given equation by factoring. is,

b.
The x-intercepts,zeros, roots and solutions are same things.
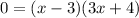
Equate each factor equal to 0.
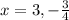
Therefore x-intercepts,zeros, roots and solutions of the given equation are
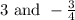 .
.
c.
The given equation is
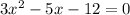
Therefore the solution of the equation are
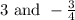 .
.