Answer:
C. The discriminant is negative, so there are no solutions.
Explanation:
We see that the given figure is a graph of a parabola.
The equation of the given parabola is
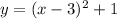 .
.
Simplifying the equation in quadratic form, we get,
The equation is
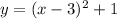 i.e.
i.e.
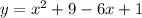 i.e.
i.e.
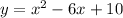 .
.
We know that the discriminant of a quadratic equation
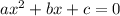 is given by
is given by
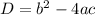
So, from the equation
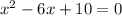 , we have,
, we have,
a = 1, b = -6 and c = 10
Thus, the discriminant is

i.e.
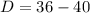
i.e.
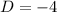
So, the discriminant is -4 i.e. negative.
Hence, as the discriminant is negative, there are no solutions.