Answer:
Q1 - x = -2 and
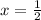
Q2 -
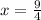 and
and
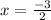
Q3 - Square, Length = 19 m
Explanation:
Question 1:
We have the equation
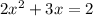 i.e.
i.e.
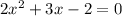
The solution of equation
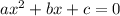 is
is
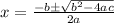 .
.
So, from the given equation, we get,
a = 2, b = 3 and c = -2.
Thus,

i.e.
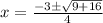
i.e.

i.e.

i.e.
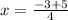 and
and
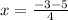
i.e.
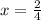 and
and
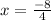
i.e.
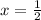 and x= -2
and x= -2
Question 2:
We have the equation
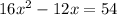 i.e.
i.e.

Again, we have,
a = 16, b = -12 and c = -54
Thus,
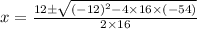
i.e.
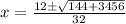
i.e.
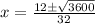
i.e.
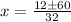
i.e.
 and
and
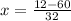
i.e.
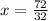 and
and
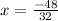
i.e.
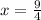 and
and
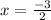
Question 3:
We have that,
Area of the rooftop =
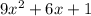
This gives us that a = 9, b = 6 and c = 1
Thus,

i.e.
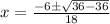
i.e.
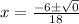
i.e.
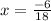
i.e.
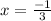
So, the area of rooftop = length × width =
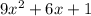 =
=
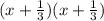 .
.
Thus, we get,
Length of the rooftop = Width of the rooftop =
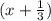
Hence, the quadrilateral is a SQUARE.
Since, the area of the rooftop is given as 361 m².
So,
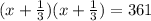
i.e.
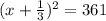
i.e.
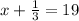
i.e.
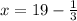
i.e.
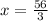
So, the length of one side is
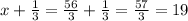
Hence, length of one side of the rooftop is 19 meter.