Question

An object on the surface of the earth weights 90lb at three radii above the surface it will weigh

Answer 1

10 lb. I got it right on a test.....

Step-by-step explanation:

Answer 2

At 3 radii above surface, the scale would display 5.6lb.

Step-by-step explanation:

An object that is said to weigh 90lb, has--due to the gravitational force at Earth's surface-- a gravitational weight of 40.8kg * 9.8 m/s^2 = 400N. This means it is pulled by the gravity toward the center of the Earth with a force of 400N. The gravity follows Newton's formula:

`F = G(m_o\cdot m_E)/(r^2)`

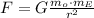
where G is an empirical constant mo is the mass of the object (NOT its "weight"), mE is mass of the Earth, and r is the radius from the center of the Earth. So we know that:

`G(m_o\cdot m_E)/(r^2)=400N`

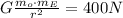
and at a distance extended by 3 more r's it is going to be:

`G(m_o\cdot m_E)/((4r)^2)=G(m_o\cdot m_E)/(16r^2)=x`

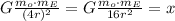
If you divide both equations and isolate x you will conclude that the gravity at 3 radii above the surface will be 400/16, or 16 times smaller. That would be the clean answer - the gravity (measure in Newtons) will be 25N. If you use the same scale to proclaim the "weight" in pounds, you will observe that the measurement of 90lb will become also 16 times smaller, or about 5.6lb, which would be the answer to the question as posted. Please note that weight should not be mixed up with mass, but the wording of this question is really not helping keeping things clean.