Question

Solve by completing the square.

Answer 1

Completing the square is a method used to solve quadratic equations.

When do this, we want a perfect square trinomial on the left side.

First get rid of the constant by subtracting 12 from both sides.

This gives us s² - 8s ___ = -12 ___.

Notice that I left room for a space.

The number that goes inside the space will be the number

that is needed to create a perfect square trinomial.

So what is that number?

Well it comes from a formula.

The number that goes in the space will be half

the coefficient of the middle term squared.

Half of -8 is -4 and if we square -4, we get +16.

So a +16 goes in each blank.

So we have s² - 8s + 16 = -12 + 16.

Now the left side factors as (s - 4)² and the right side simplifies to 4.

So we have (s - 4)² = 4.

Now get rid of the squared by square rooting both sides.

So
`\sqrt{(s - 4)^(2)} = √(4)`.

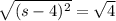This gives us s - 4 = ±2.

Don't forget to use plus or minus when

square rooting both sides of an equation.

So either s - 4 = 2 or s - 4 = -2.

Solving each equation from here, we get s = 2 or s = 6.

Let's write our answer inset notation.

{2, 6}.

Answer 2

The correct answer is Option A. {2,6}

Explanation:

Let the given equation be,

s² -8s + 12 =0 ----(1)

⇒s² -8s = -12 ----(2)

Here coefficient of x, b = -8

b/2 = -8/2 = -4

(b/2)² = 16

add 16 on both the sides of equation (2)

s² -8s + 16 = -12 + 16

s² -8s+ 16 = 4

(s - 4)² = 2²

s - 4 = ± 2

s = +2 + 4 = 6 or s = -2 + 4 = 2

Option A. {2,6} is the correct answer