Answer:
Because the mass of electrons and protons is very small
Step-by-step explanation:
The gravitational force exerted between two objects is given by:
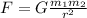
where
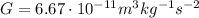 is the gravitational constant
is the gravitational constant
m1 and m2 are the masses of the two objects
r is the distance between the two objects
The mass of a proton and of an electron is very small, so the gravitational force involved in case of such particles is very weak. Let's calculate for example the gravitational attraction between one proton and one electron at a distance of r = 1 m. We have:
- Proton mass:
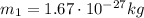
- Electron mass:
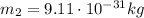
So, the gravitational force between the two particles is:
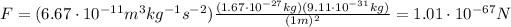
Which is a very weak force.
By comparison, let's calculate instead the electromagnetic force between a proton and an electron (both having a charge of
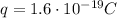 ) still separated by a distance of r = 1 m. We have:
) still separated by a distance of r = 1 m. We have:
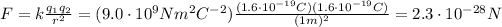
Which we see is much stronger than the gravitational force (almost by a factor
