1) If the limit
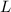 is
is
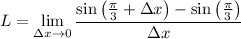
then using the hint as well as
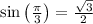 and
and
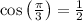 we have
we have
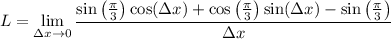
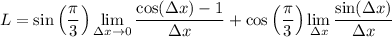

which follows from the well-known limits,
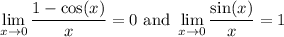
Alternatively, if you already know about derivatives, we can identify the limit as the derivative of
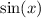 at
at
 , which is
, which is
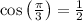 .
.
2) It looks like you may be using double square brackets deliberately to denote the greatest integer or floor function which rounds the input down to the nearest integer. That is,
![[\![x]\!]](https://img.qammunity.org/2023/formulas/mathematics/college/snkfcy66um065wuajzov9qgb3ghddin88r.png) is the greatest integer that is less than or equal to
is the greatest integer that is less than or equal to
 . The existence of
. The existence of
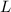 depends on the equality of the one-sided limits.
depends on the equality of the one-sided limits.
Suppose
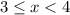 . Then
. Then
![2[tex]\displaystyle \lim_(x\to4^-) [\![x - 1]\!] = 2](https://img.qammunity.org/2023/formulas/mathematics/college/3o086f4j30bocxj4x8f92u0btiugzdo8i8.png)
Now suppose
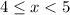 , so that
, so that
![3\le x-1 < 4 \implies [\![x-1]\!]=3](https://img.qammunity.org/2023/formulas/mathematics/college/kf6y39hmascnmlxv3biz671xcjcbszxrqq.png) and
and
![\displaystyle \lim_(x\to4^+) [\![x-1]\!] = 3](https://img.qammunity.org/2023/formulas/mathematics/college/5jwa90xad3785f7ozcytnm9h8tb02ew41t.png)
The one-sided limits don't match so the limit doesn't exist.