Question

A ladder is leaning against a wall and make an 82 degree angle of elevation with the ground.

Part A: If the base of the ladder is 4 feet from the wall, then how long is the ladder? Round to the nearest tenth.
Part B: Determine how high up the wall does the ladder reach.

Answer 1

A) The length of Ladder is 28.7 feet.

B)The length of the wall up to where the ladder reaches is 28.5 feet.

Explanation:

Consider a wall AB and a ladder AC .

The ladder is leaning against a wall and make an 82 degree angle of elevation with the ground that is ∠ACB = 82°

Part A) If the base of the ladder is 4 feet from the wall that is BC= 4 feet.

We have to find the length of ladder (AC).

Consider Δ ABC , with ∠B= 90°

Applying trigonometric ratio,

`\cos C=\frac{\text{Base}}{\text{Hypotenuse}}`

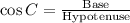
Substitute the values, we get,

`\cos C=(BC)/(AC)`

`\Rightarrow \cos 82^(\circ)=(4)/(AC)`

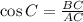
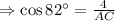
Solve for AC, we get,

`\Rightarrow AC=(4)/(\cos 82^(\circ))`

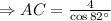
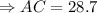`\Rightarrow AC=28.7` (approx)

Thus, the length of Ladder is 28.7 feet.

B) To determine the length of the wall up to where the ladder reaches,

Applying trigonometric ratio,

`\tan C=\frac{\text{Perpendicular}}{\text{Base}}`

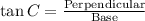
Substitute the values, we get,

`\tan C=(AB)/(BC)`

`\Rightarrow \tan 82^(\circ)=(AB)/(4)`

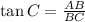
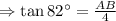
Solve for AB, we get,

`\Rightarrow AB=\tan 82^(\circ) * 4`

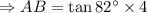
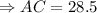`\Rightarrow AC= 28.5` (approx)

Thus, the length of the wall up to where the ladder reaches is 28.5 feet.