Answer: The correct option is (A)
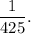
Step-by-step explanation: We are given to consider an example of a deck of 52 cards.
We are to find the probability of drawing three queens from a standard deck of cards, given that the first card drawn was a queen and the cards are not replaced.
We know that there are 4 queens in a deck of 52 cards.
Since the first card is already a queen and the cards are not not being replaced, so we have 3 options for 2nd queen and 2 options for 3rd queen.
That is, the total number of options for three queens is given by
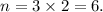
Now, after drawing first queen, 51 cards left in the deck and after drawing second queen, 50 cards left in the deck.
So, the probability of drawing three queens from a standard deck of cards, given that the first card drawn was a queen is
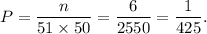
Thus, the required probability is
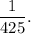
Option (A) is correct.