Answer:
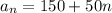
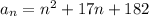
Explanation:
We have been given two sequence:
200,250,300,350,400,450
200,220,242,266,292,320
In first sequence We can see that there is common difference of 50 between consecutive terms:
So, we can use the formula of arithmetic sequance which is:
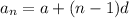
Where, a is first term and d is common difference n is the number of terms:
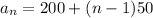
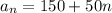
Now, for second sequence:
200,220,242,266,292
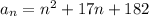 is the iterative rule
is the iterative rule
If we put n=1 in above formula we will get
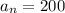
At n=2,
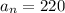
And so on... by substituting consecutive values as in sequence given.