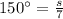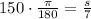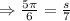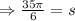Answer:
We will find the arc length of the given circles.
By using
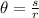
And also
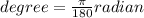
Where, s is the arc length and r is the radius.
In figure 3 : radius is 9 yd and
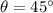
On substituting the values in the formula we get:
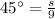

In figure 4:radius is 11 km and
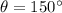
On substituting the values in the formula we get:
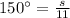
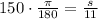
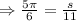

In figure 5:radius is 11 in and

On substituting the values in the formula we get:
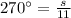
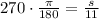
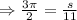
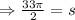
In figure 5:radius is 11 in and

On substituting the values in the formula we get:
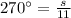
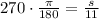
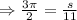
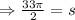
In figure 6:radius is 7 in and
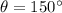
On substituting the values in the formula we get: