Question 14
As we approaching from the negative side,
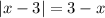 .
.
So, we have
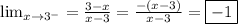
and thus the limit exists at x=3.
Question 15
For the top part of the function,
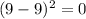
For the bottom part of the function,
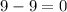
As both one-sided limits are equal, L = 0, and thus the limit exists at x=9.