Question

Solve for z square root of z^2-8- square root of 6z-17=0

Answer 1

Explanation:

`√(z^2-8) -√(6z-17) =0\\√(z^2-8) =√(6z-17) \\6z > 17\\z > (17)/(6) \\z^2-8=0\\z^2 > 8\\so \\z < -√(8) \\or\\z > √(8) \\combining\\z > (17)/(6) \\again\\z^2-8=6z-17\\z^2-6z-8+17=0\\z^2-6z+9=0\\z^2-3z-3z+9=0\\z(z-3)-3(z-3)=0\\(z-3)(z-3)=0\\z=3`

Answer 2

`\large\displaystyle\text{$\begin{gathered}\sf \sqrt{z^(2)-8 }-√(6z-17)=0 \end{gathered}$}`

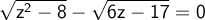
Simplify the left side. Yes n is a positive integer greater than x and a is a real number or a factor, then
`\bf{\sqrt[n]{a^(x) }=a^{(x)/(n) }. }`

`\large\displaystyle\text{$\begin{gathered}\sf \bf{(z^(2)-8)^{(1)/(2) }-√(6z-17)=0 } \end{gathered}$}`

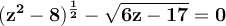
If n is a positive integer greater than x and a is a real number or a factor, then
`\bf{\sqrt[n]{a^(x) }=a^{(x)/(n) }. }`

`\large\displaystyle\text{$\begin{gathered}\sf \bf{(z^(2)-8)^{(1)/(2) }-(6z-17)^{(1)/(2)} =0 } \end{gathered}$}`

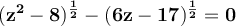
Draw each side of the equation. The solution is the x value of the point of intersection.

`\red{\underbrace{\overbrace{\boxed{\boldsymbol{\sf{\green{z=3}}}}} \ \ \to \ \ \ Answer}}`

{ Pisces04 }